String Matching

當我們需要比較兩個字串是否一致時， 其實我們就像是在比較兩個數字陣列是否一致， 只是從一般的數字變成 ASCII Code 組成的陣列。

如果我們不在乎順序，這是一個很簡單的問題，我們只要比較每個字元出現次數， 反之，我們只能逐一比較，除了長度不一樣可以明顯區分的情況以外， 需要花費 $O(|S|)$ 的時間比較，在多組比較下時間非常慢， 因此我們需要一些快速的比較方式。

Hashing

我們第一個想法是比較很多數字太浪費時間了， 可不可以把一個字串壓成一個數字？

回想數字進制的表示法！ 我們其實可以參考數字進位的方式，像是十進位的 $163=10^2\times 1+10^1\times 6+10^0\times 3$， 用類似的方式，找到一個比字元集 $\sum$ 大小大的數字 $B$，例如只有小寫的話我們取 $29$， 字串 $abaa$ 就可以表示成 $29^3\times 1+29^2\times 2+29^1\times 1+29^0\times 1$，'a' 對應 $1$，'b' 對應 $2$。

這樣有一個問題，假設字串長度是 $10^3$ 甚至 $10^5$， $29^{999},29^{99999}$ 這麼大的數字我們要如何儲存跟計算？即使透過 Python 或者其他語言的大數來處理， 這個所花費的空間仍然是非常驚人的，所以我們希望出來的數字不要太大。

我們可以透過模除的方式，將這個結果模除一個數字 $P$，這樣結果的範圍就會被壓縮在 $[0,P)$ 內， 同時因為這個數字的計算過程只用到乘法和加法， 透過模除定理我們可以在計算過程中保證每一步的數值不會太大。 將一串指定內容轉變成數字的函數我們稱為雜湊 (Hashing)，用 $\text{Hash}(S)$ 表示。

接著就產生一個新的問題，如果用大數來存，我們可以保證當兩個結果數字一樣時， 字串內容一定一樣，但是現在就不行了，因為模除等同於把數字壓縮到一個有限的範圍內， 這樣就可能有不同的字串算出一樣的結果， 這個情況稱為碰撞 (Collision)。

碰撞處理

我們的底數 $B$ 以及模數 $P$，選擇質數。

$B$ 選擇一個略大於字元集合大小的質數，
$P$ 選擇接近 $10^9$ 的質數，像是 $10^9+7,10^9+9,998244353$。

如果 $B$ 跟 $P$ 有公因數，那麼 $B^i\mathrm{mod}P$ 會很快出現重複， 導致很多不同的字串對應到相同的哈希值（碰撞變多）。

舉例： 若 $P=10,B=5$ 那 $5^1=5,5^2=25$, $5^1{\equiv }_{10}{5}^2$ 若 $B$ 是質數、且與 $P$ 無公因數，$\mathrm{mod}P$ 後的分布會比較隨機，讓結果更平均、碰撞機率更低。

假設要進行 $m$ 次比較，模數為 $P$，碰撞的機率大約是 $\frac{m^2}{2P}$， 所以只選擇一個質數 $P$ 的話，當 $m$ 很大時，碰撞機率也會變得很高， 我們可以選第二個質數 $P^{\prime }$，做第二次 Hash，每次比較兩個 Hash 值。

const int B = 29, P = 998244353;
long long hash(const string &s)
{
    long long res = 0;
    int n = s.size();
    for(int i = 0; i < n; ++i)
        res = ((res * B) % P + s[i]) % P;
    // 自己想看看，為何這樣就可以達成我們要的效果，而不需要快速冪。
    return res;
}

Rolling Hash

剛才講的例子是直接比較兩個完整字串 $S,T$ 是否一致， 一個更通用的情況是，在字串 $S$ 中尋找是否有子字串 $T$，或者檢查出現幾次， 我們稱為字串匹配。

我們如果對字串 $S$ 中所有長度為 $|T|$ 的子字串做 Hashing，然後一一比較，
總時間複雜度為 $O((|S|-|T|)\times |T|)=O(|S||T|)$，聽起來真的是有夠糟糕的， 但如果我們觀察一下相鄰的兩個長度為 $T$ 的子字串，可以發現一些端倪。

假設我們有字串 $abda$，兩個長度為三的子字串分別為 $abd,bda$， 假設輸出都挺小的，我們都先省略模除的部份，他們的 Hash 分別為

$B^2\times 1+B^1\times 2+B^0\times 4$,
$B^2\times 2+B^1\times 4+B^0\times 1$，

完整字串 $abda$ 的 Hash 是

$B^3\times 1+B^2\times 2+B^1\times 4+B^0\times 1$，

子字串 $bda$ 的 Hash 值剛好是完整字串拿掉 $B^3\times 1$， 子字串 $abd$ 的 Hash 值剛好是完整字串拿掉 $B^0\times 1$ 然後同除 $B$， 講到這裡，你應該有發現子字串的雜湊值，可以透過類似於前綴和抵銷的方式快速算出來， 因為消掉前面比起消掉後面多餘的好做， 所以如果我們在每次計算 Hash 的時候，同時存下每一個前綴字串的 Hash 值， 我們就可以透過前綴 Hash 值來計算任意子字串的 Hash 值。

我們計算好字串 $abda$ 的五個前綴 hash 值：
$\text{prefHash}(S[\mathrm{0..0}])=0$
$\text{prefHash}(S[\mathrm{0..1}])=B^0\times 1$
$\text{prefHash}(S[\mathrm{0..2}])=B^1\times 1+B^0\times 2$
$\text{prefHash}(S[\mathrm{0..3}])=B^2\times 1+B^1\times 2+B^0\times 4$
$\text{prefHash}(S[\mathrm{0..4}])=B^3\times 1+B^2\times 2+B^1\times 4+B^0\times 1$

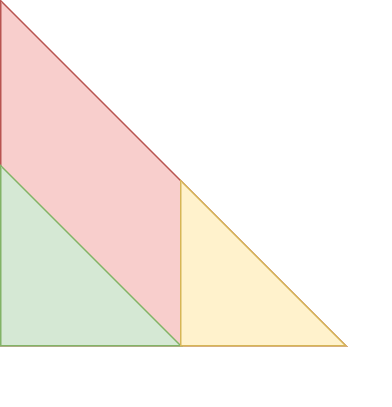
在圖形上來看會呈現一個三角形，所以被消去的部份要往上放大。

子字串 $abd$ 的 $\text{Hash}(S[1:3])$ 就是 $\text{prefHash}(S[3])-\text{prefHash}(S[0])\times B^{3-1+1}$
子字串 $bda$ 的 $\text{Hash}(S[2:4])$ 就是 $\text{prefHash}(S[4])-\text{prefHash}(S[1])\times B^{4-2+1}$

至此，如果我們存下每一個前綴 Hash 值，可以在 $O(1)$ 時間算出所有子字串的 Hash 值， 記得要加上模除，因為有減法，出來可能有負值，記得先模除再加上 $P$ 轉回 $[0,P)$， 另外 $B^i$ 可以在一開始邊做前綴 hash 的時候存下來，這樣就不用快速冪了。

結論

字串 Hash 就是最簡單但不穩定的作法， 之後介紹的演算法就是穩定的做法， 但只會雜湊也夠打天下了。

KMP 字串匹配演算法 (Knuth-Morris-Pratt)

字串匹配是指在一個主字串 $S$ 中尋找模式字串 $T$ 是否出現。 直覺的暴力作法 (Brute Force) 是將兩個字串對齊，一一比較。

為什麼暴力法太慢？

假設 $S=\text{"ababcababd"}$, $T=\text{"ababd"}$

S: a b a b c a b a b d
T: a b a b d
   ^ ^ ^ ^ x (在 index 4 失敗)

當我們在 'd' 失敗時，我們已經知道前面 "abab" 是匹配成功的。 暴力法會把 $T$ 往右移一格重新比較，這浪費了我們已經知道 "abab" 匹配的資訊。時間複雜度高達 $O(|S||T|)$。

核心觀念：Failure Function ($\pi$)

我們能不能直接滑動多格一點？ 觀察已匹配的 "abab"：

• 它的前綴 (Prefix) 有：a, ab, aba...
• 它的後綴 (Suffix) 有：b, ab, bab...
• 最長的相同前後綴是 "ab"。

這表示目標字串 $T$ 的開頭 "ab" 可以跟目前已經匹配的 "abab" 的後綴 "ab" 對齊， 這樣讓我們可以直接把 $T$ 往右滑動兩格，減少一些不必要的比較。

我們定義 $\pi [i]$： 表示子字串 $T[\mathrm{0..}i]$ 中，最長的「相等的真前綴與後綴」長度。

第零格沒有意義，因為只有一個字元沒有真前綴或真後綴。

那麼 $\pi$ 有什麼方法可以快速計算呢？ 藉助 Hashing 的技巧，我們可以二分搜 $\pi [i]$ 的值，這樣是 $O(|T|\log |T|)$， 雖然這樣已經足夠快了，但是我們剛才說了 Hash 有碰撞的問題，所以還是希望可以找到一個乾淨的解法。

跟剛才的想法一樣，能榨乾已經計算好的資訊就盡量榨乾它。 我們透過幾個例子來看看怎麼利用已知的 $\pi$ 值來計算新的 $\pi$ 值。

假設已經算好前三格的 $\pi$ 值，我們要算第四格的 $\pi [4]$， 我們知道第三格的 $\pi [3]=2$，代表 $T[\mathrm{0..3}]$ 的最長相等前後綴長度是 $2$， 也就是 "ab"。

當我們有新的字元 'a' 要加入計算時，我們可以檢查 'a' 是否等於 $T[\pi [3]]=T[2]$， 因為 'a' 加入後，$\pi [3]$ 告訴我們目前已經有長度為 $2$ 的相等前後綴，我們可以直接檢查下一個字元是否相等。

T: a b a b a c
       ^     (檢查 T[4] 與 T[2] 是否相等)

根據檢查結果，我們可以更新 $\pi [4]$：

• 相等：$\pi [4]=\pi [3]+1=3$

接著我們要算第五格的 $\pi [5]$， 我們同樣從 $\pi [4]=3$ 開始檢查， 檢查 'c' 是否等於 $T[\pi [4]]=T[3]=$ 'b'， 發現並不相等，那我們就要從頭開始找了嗎？

既然 T[0..4] 的最長相等前後綴不能用，我們就找第二長的相等前後綴， T[0..4] 的前綴有 a, ab, aba, abab
後綴有 a, ba, aba, baba

最長的相等前後綴是 "aba"，長度為 $3$，也就是 $\pi [4]=3$ 告訴我們的結果， 第二長的相等前後綴是 "a"，所以我們可以嘗試檢查 'c' 是否等於 $T[1]=$ 'a'。

T: a b a b a c
     ^     (檢查 T[5] 與 T[1] 是否相等)

很可惜還是不相等，那我們就只能找第三長的相等前後綴了， 但是 T[0..4] 的相等前後綴已經找完了，所以 $\pi [5]=0$，代表沒有相等的前後綴。

另外，我們也可以發現一件事情，次長的相等前後綴 "a" 其實是最長相等前後綴 "aba" 的一部份，甚至其實就是 $\pi [2]$ 的結果， 所以當我們在找次長、三長的相等前後綴時，我們可以直接利用 $\pi$ 函數來幫助我們找到下一個候選者，也就是 $\pi [\pi [i-1]-1]$。

當我們的 $\pi$ 產生回退的時候，代表有新的字元產生了 障礙，讓我們無法延續之前的相等前後綴， 即使重新開始延伸，我們也無法跨過這個障礙，用存錢的概念來說，這個障礙就像是存錢的提款機一樣， 我們回退（領錢）不可能超過之前存的錢（已經計算好的 $\pi$ 值），而 $\pi$ 最多就是 $|T|-1$， 所以回退的過程加往前的過程總共不會超過 $O(|T|)$，整個 $\pi$ 函數的計算時間就是線性的 $O(|T|)$。

vector<int> computePi(const string &T)
{
    int n = T.size();
    vector<int> pi(n);
    for(int i = 1; i < n; ++i)
    {
        int j = pi[i - 1];
        while(j > 0 && T[i] != T[j])
            j = pi[j - 1];
        if(T[i] == T[j])
            ++j;
        pi[i] = j;
    }
    return pi;
}

$\pi$ 函數就可以在 $O(|T|)$ 的時間完成計算了， 接著我們就可以透過 $\pi$ 函數來進行字串匹配，總時間複雜度為 $O(|S|+|T|)$。

當然其實我們可以不用那麼麻煩，只要透過一個不在字元集合內的字元把兩個字串接起來， 例如 $T+\text{!}+S$，直接對它進行 $\pi$ 的計算， 有一個位置的配對長度 $=|T|$ 就代表找到一個配對。

Z Value (Z Algorithm)

這裡要介紹另外一個用來字串匹配的演算法 Z algorithm， 我們對於每個字串的位置 $i$ 求出，從第 $i$ 個字元開始的子字串，與整個字串的前綴，最長可以匹配到哪裡。

這樣也可以幫助我們快速移動匹配的字串，當然，我們也可以一樣透過 $T+\text{!}+S$，直接對它進行 $\text{Z}$ 的計算， 有一個位置的配對長度 $=|T|$ 就代表找到一個配對。

接下的問題就是要如何快速計算 Z 函數了， 例子 aabxaabxcaabxaabxay

跟 KMP 一樣，第一格沒有意義

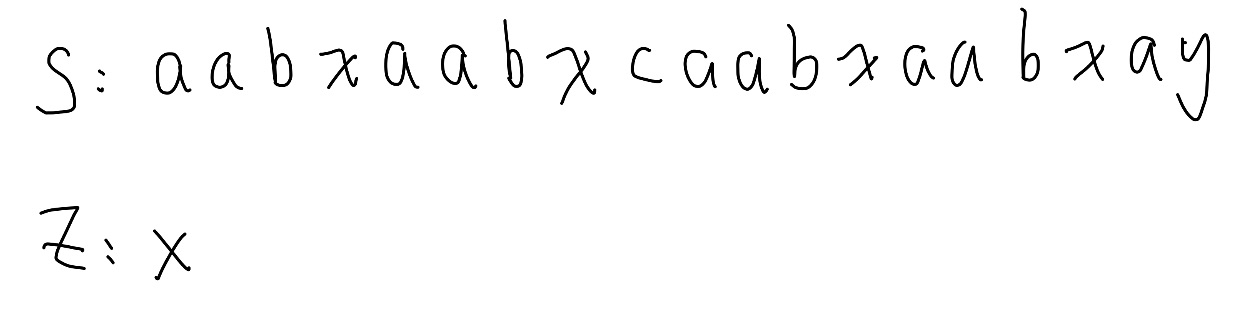
前面幾個很快可以看出來，我們先快轉

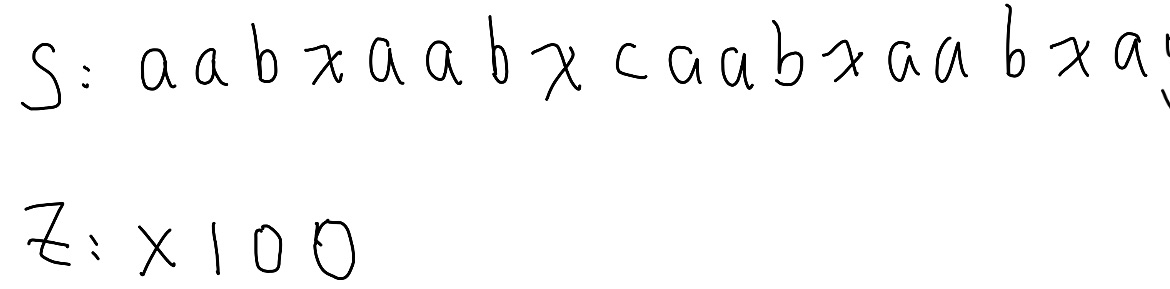
到這裡時，我們會有長度為四的匹配，產生的匹配區間我們稱為 Z box，

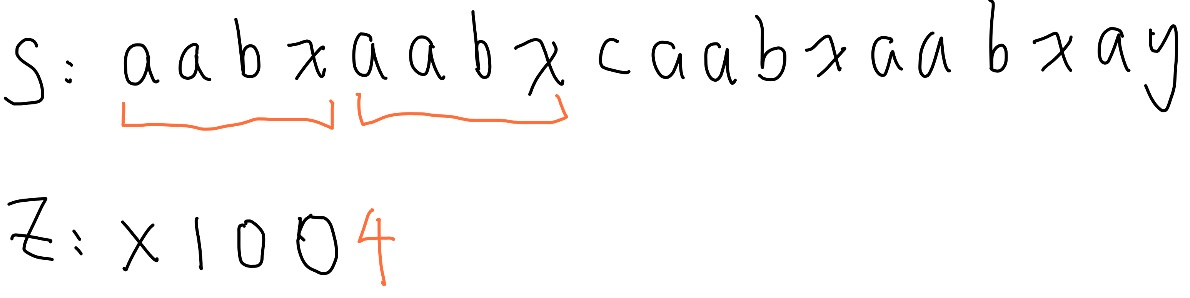
Z box 內的資訊可以由字串開頭得知，直接照抄

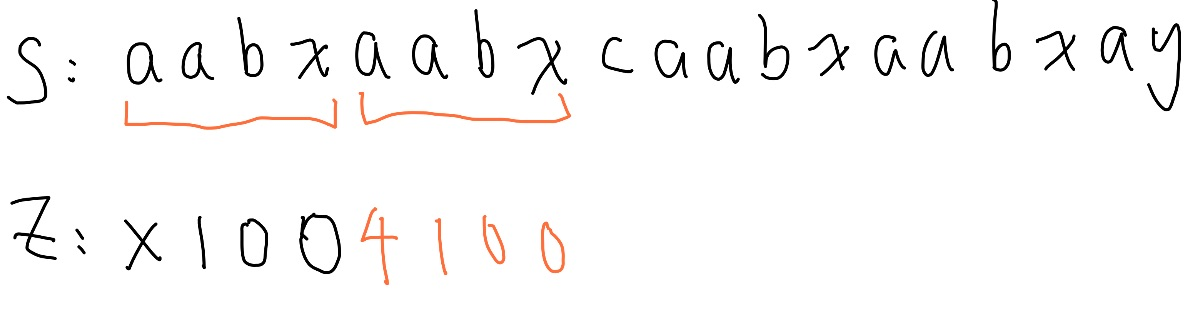
超出 Z box 了，重新比較，直到發現新的 Z box，

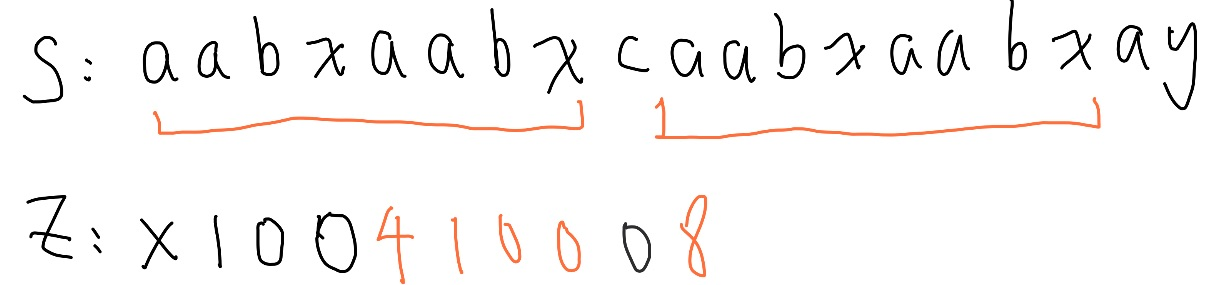
照抄下來，發現這個位置前綴中填四，但實際上還可以往後延伸， 當 $z(i{)}^{\prime }+i$ 貼齊 Z box 右邊界時，代表其實我們有可能可以繼續延伸， 因為 Z box 是井底之蛙，我們只能知道 Z box 內的資訊，無法得知 Z box 外的資訊。

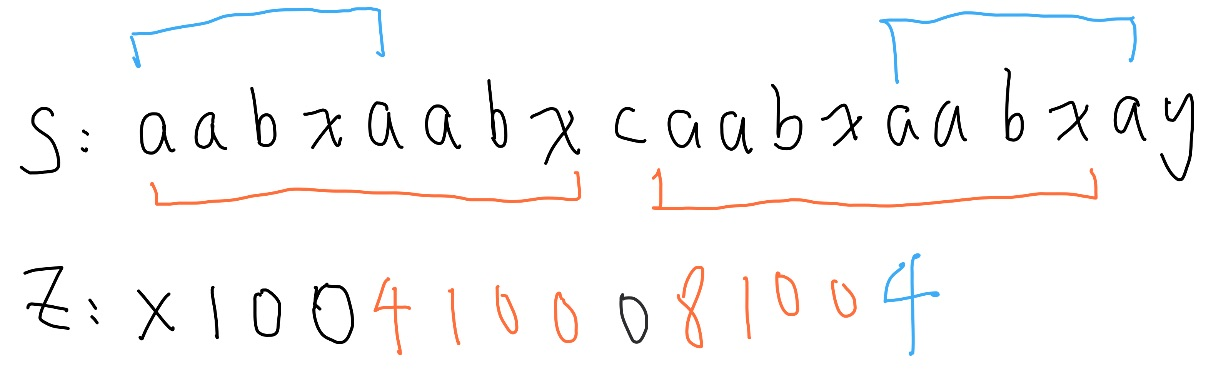
從 Z box 右邊界開始繼續比較，嘗試延伸後更新 Z box

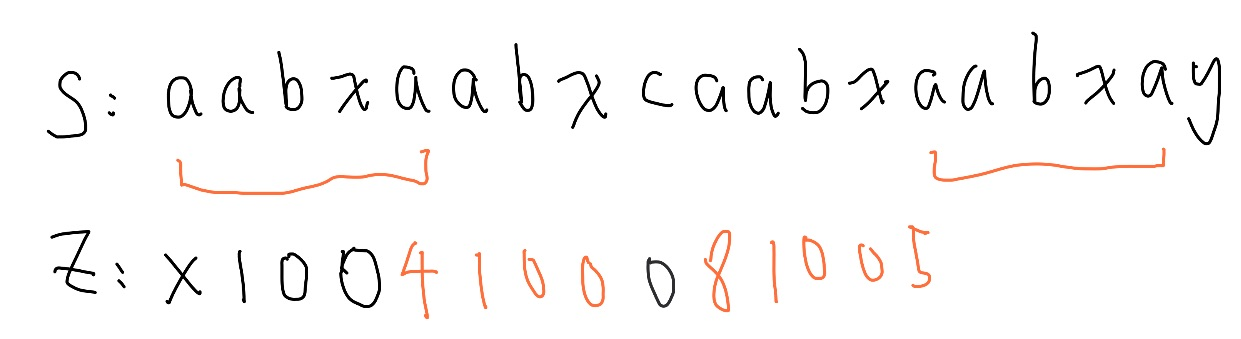
照抄下來，又有一個不對勁的地方，如果 $z(i{)}^{\prime }+i$ 超過 Z box 右邊界， 我們反而要縮回來，一樣從 Z box 右邊界開始比較後更正。

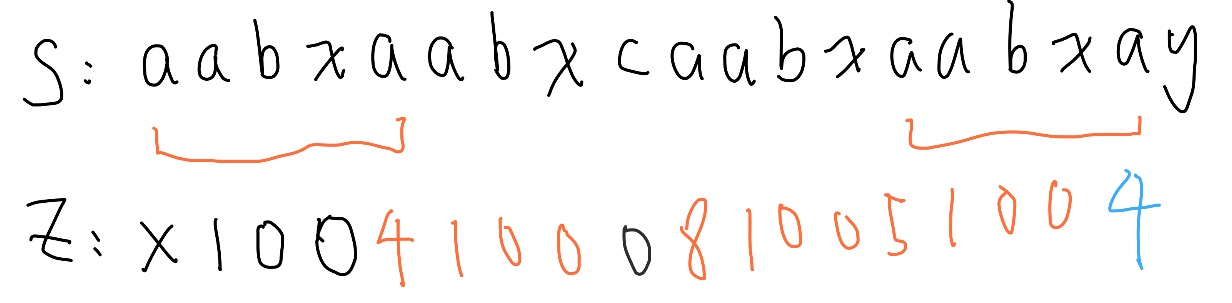
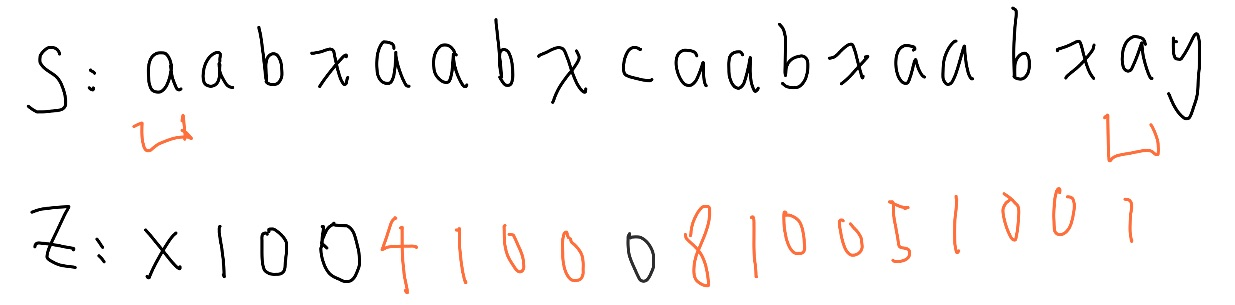
完成 Z value 的計算。

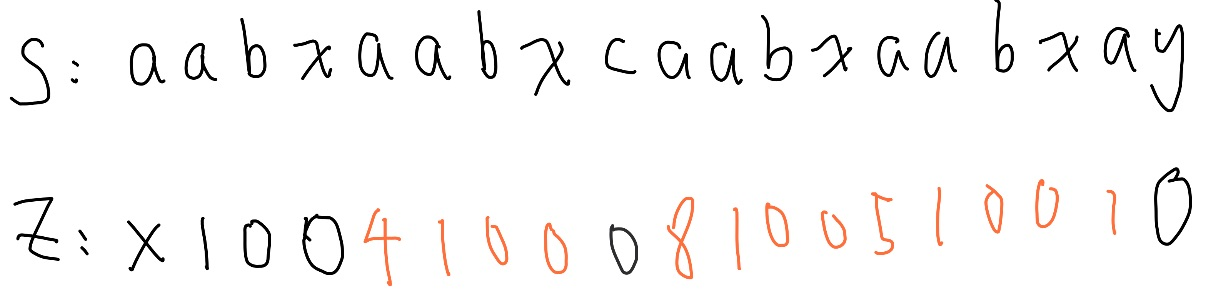
因為 Z box 只會不斷往右移動，自然也沒有不斷來回從頭比較的必要， 所以 Z algorithm 的時間複雜度肯定是線性的 $O(|T|)$。

在部分的網站中，有些人會稱 Z value 為擴展 KMP (Extended KMP)， 但其實這兩個演算法是獨立發展出來的，沒有什麼關係，剛好可以用來解決同一個問題， 另外筆者個人認為 Z algorithm 比 KMP 更直觀易懂一些，但還是推薦都要學會，字串眼萬法算是台灣比賽的必考題型。

因為實作比較直覺，這裡留給讀者自行實作。

題單

• CSES String Matching
• CSES String Functions
• CSES Finding Borders
• CSES Finding Periods
• Codeforces Password