Trie 字典樹
KMP 以及 Z value 等做法在一對一時很好用,線性的做法基本上是無人能敵, 但假設我們的問題變成下面這樣,就顯得有點不足了:
給定 個字串,對於每個字串我們要計算出這個字串總共作為幾個字串的前綴出現, 例如 "abc","ab","bc","b" 的答案就是 1, 2, 1, 2。
兩兩之間做字串匹配演算法顯然不夠有效率,因此我們要在這裡介紹可以有效處理這個問題的資料結構:字典樹 Trie,也稱為前綴樹。
正如其名,這個資料結構是樹形的,以空字元為根,第 層的節點代表存在一個字串的第 個字元為 。
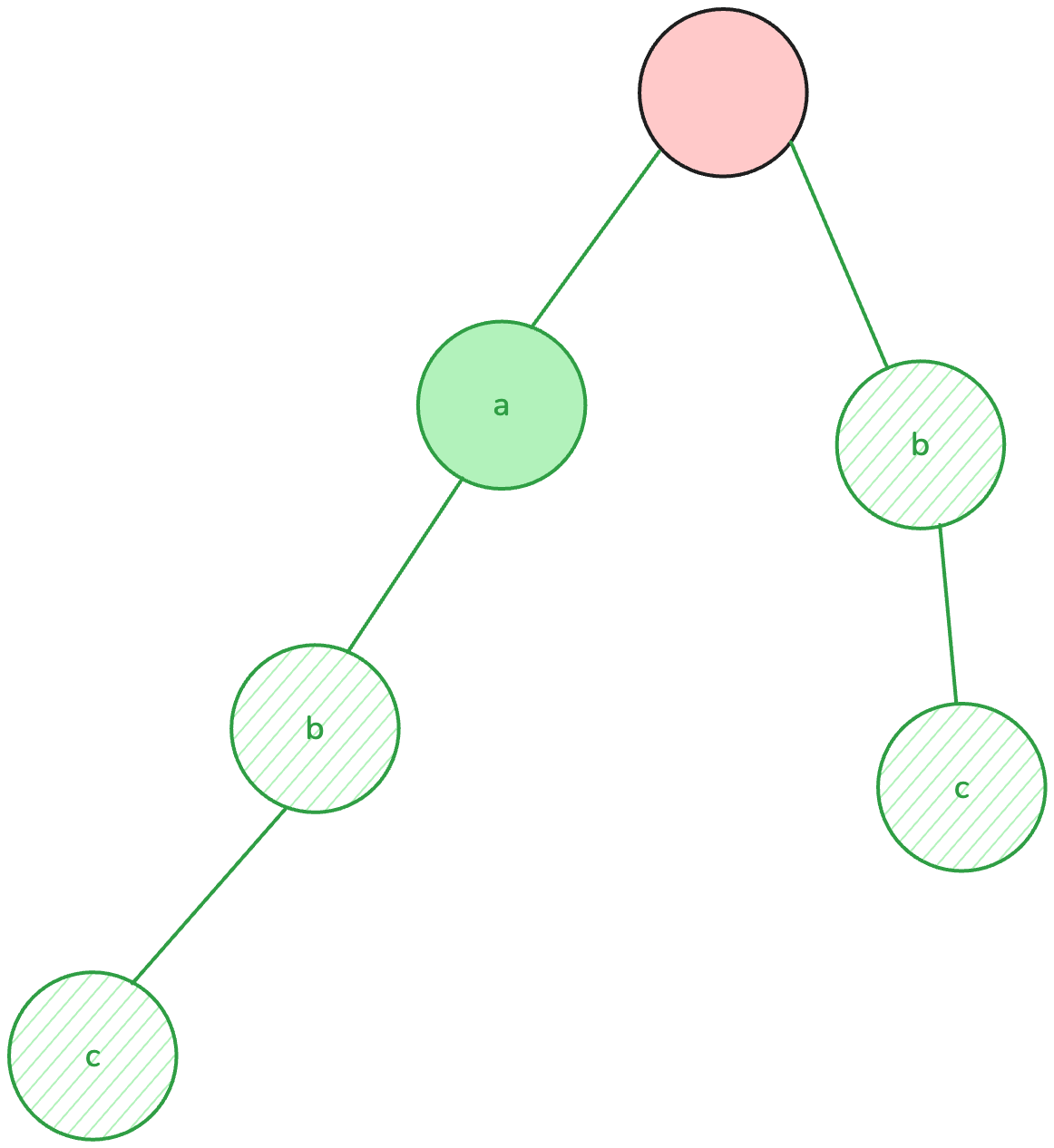
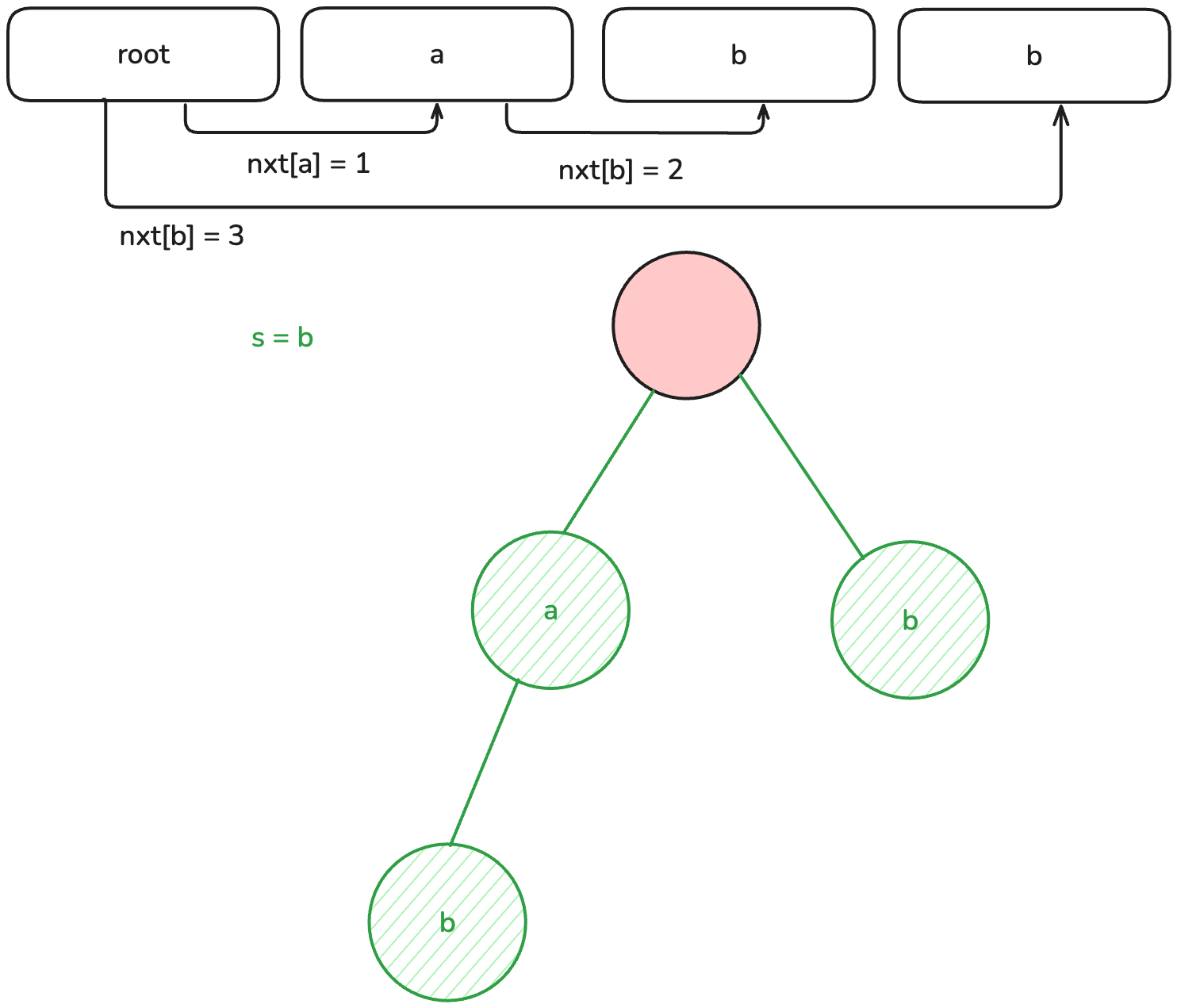
斜線背景的節點代表有字串的結尾在此,幾設今天要詢問的不是單純前綴,而是問字串 是否出現過, 這時詢問字串 "a" 如果沒有適當的處理,會誤以為有出現過,但是節點有標記是否為結尾的話,就可以很好的分辨。
我習慣用類似這樣的結構代表節點:
const int CHARSET = 26
struct Node
{
int nxt[CHARSET] = {};
bool is_end = false;
// 其他需要儲存的資訊
};
nxt 用來儲存下一層節點的指向,也許你會問為何不用指標?因為指標比較浪費空間,
當然我也不建議使用類似於 int trie[N][CHARSET] 的陣列存儲字典樹,因為這樣要浪費 的空間,實際上不會那麼稀疏。
因為需要動態新增,這裡我會使用 vector 來達成, nxt[] 則指向下一個節點在 vector 中的索引值 (index)。
vector<Node> Trie(1, Node());
因為要有一個節點代表空,所以初始已經有一個元素。
插入
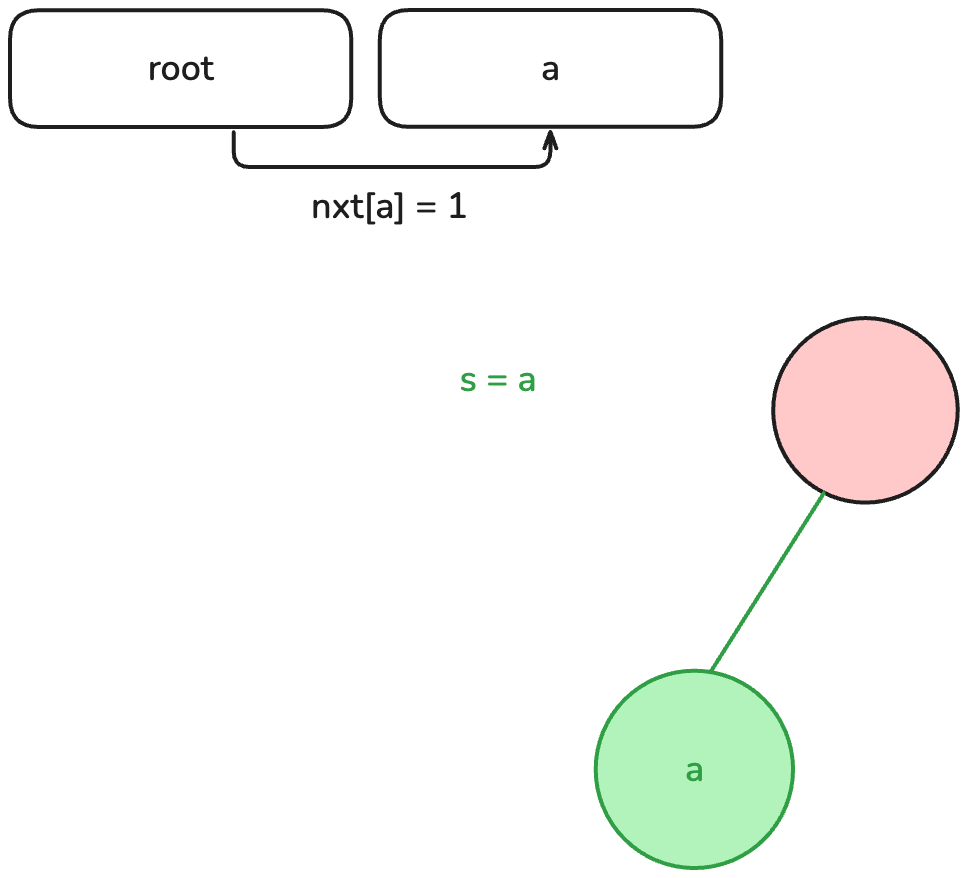
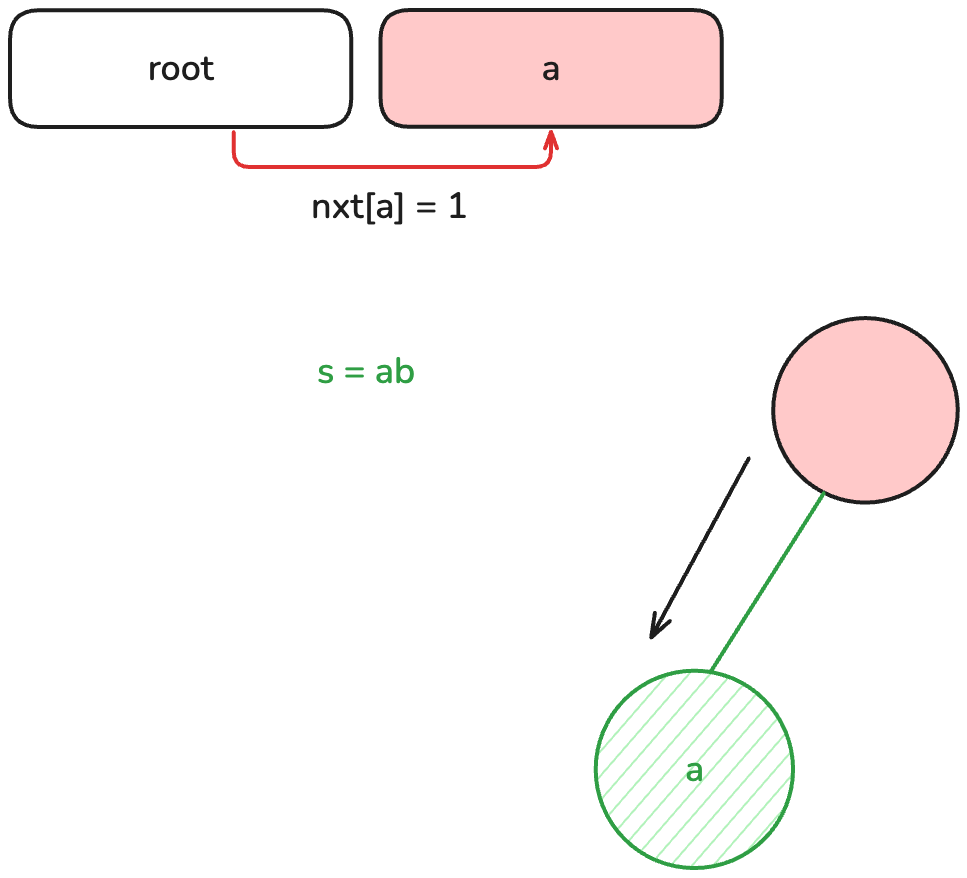
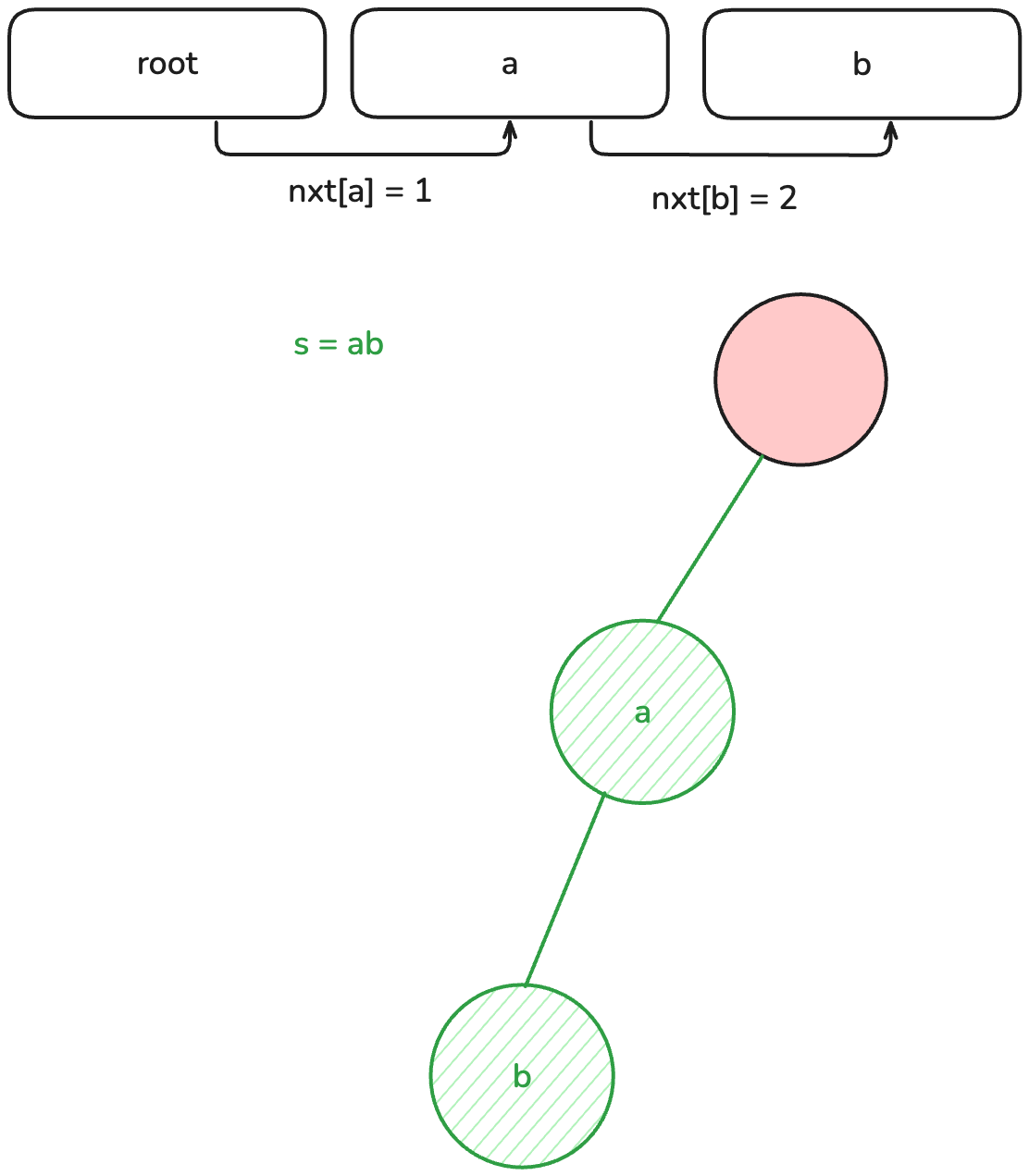
當我們有一個字串進來的時候,我們就從第一個字元開始,
如果第一個字元為 我們就檢查根節點的 nxt[c] 是否為 0,代表目前沒有這個節點,
如果已經存在,我們就朝著那個節點前進,反之,先新增一個新的節點到 vector 中。
void insert(const string &s)
{
int cur = 0;
for(char c: s)
{
if(!Trie[cur].nxt[c - 'a'])
{
Trie[cur].nxt[c - 'a'] = Trie.size();
Trie.push_back(Node());
}
cur = Trie[cur].nxt[c - 'a'];
}
Trie[cur].is_end = true;
}
那麼我們要怎麼用字典樹來求解剛才的問題?我們其實可以幫每個節點新增計數器, 當插入一個字串時,經過的節點都 。
const int CHARSET = 26
struct Node
{
int nxt[CHARSET] = {};
bool is_end = false;
int cnt = 0;
};
vector<Node> Trie(1, Node());
void insert(const string &s)
{
int cur = 0;
for(char c: s)
{
if(!Trie[cur].nxt[c - 'a'])
{
Trie[cur].nxt[c - 'a'] = Trie.size();
Trie.push_back(Node());
}
cur = Trie[cur].nxt[c - 'a'];
Trie[cur].cnt++;
}
Trie[cur].is_end = true;
}
查詢
接著我們就可以透過查詢的實作,回傳找到的 cnt 值即是答案。
int sec(const string &s)
{
int cur = 0;
for(char c: s)
{
if(!Trie[cur].nxt[c - 'a'])
return -1; // 題目是用有記錄的字串查詢,理論上不會到這
cur = Trie[cur].nxt[c - 'a'];
}
if(!Trie[cur].is_end)
return -1; // 題目是用有記錄的字串查詢,理論上不會到這
return Trie[cur].cnt;
}
在這樣的實作下,單次插入跟查詢都是 ,我們省去了跟每個字串一一比較的時間, 只需要一次遍歷即可,如果你遇到任何只跟前綴 / 後綴 (反著建) 有關的字串題目,不妨用字典樹來嘗試看看。
01-Trie
給你 個數字 ,我們希望找到一對數字 使得 最大, 可能你沒有任何的頭緒,我們先把問題簡單化,給你一個數字 如何在陣列中找到跟他 xor 後最大的數字? 我們會希望從最高位開始,跟 越不像越好,
所以如果從高位開始,用 0 跟 1 建立一棵 01 字典樹,我們的目標就變成,在字典樹上查詢,但是每次根據當前的位元, 如果有不同的位元節點就朝另外一邊走,尋找一個盡量差最多的數字,這樣我們就可以在 求解, 遠遠比直接列舉所有組合的 更有效率。